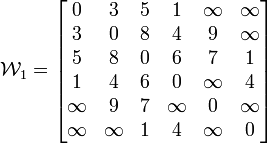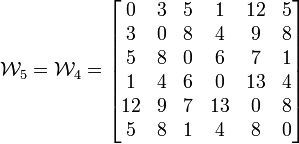viernes, 15 de febrero de 2013

Teorias explicitas y ejemplos

Algoritmo DE FLOYD

El algoritmo de Floyd es más general que el de Dijkstra, ya que determina la ruta más corta entre dos nodos cualquiera de la red.
  • El algoritmo representa una red de n nodos como una matriz cuadrada de orden n, la llamaremos matriz C. De esta forma, el valor Cij representa el coste de ir desde el nodo i al nodo j, inicialmente en caso de no existir un arco entre ambos, el valor Cij será infinito.
  • Definiremos otra matriz D, también cuadrada de orden n, cuyos elementos van a ser los nodos predecesores en el camino hacia el nodo origen, es decir, el valor Dij representará el nodo predecesor a j en el camino mínimo desde i hasta j. Inicialmente se comienza con caminos de longitud 1, por lo que Dij = i.
  • Las diagonales de ambas matrices representan el coste y el nodo predecesor para ir de un nodo a si mismo, por lo que no sirven para nada, estarán bloqueadas.
Los pasos a dar en la aplicación del algoritmo de Floyd son los siguientes: 
  • Formar las matrices iniciales C y D.
  • Se toma k=1.
  • Se selecciona la fila y la columna k de la matriz C y entonces, para i y j, con i≠k, j≠k e i≠j, hacemos:
Si (Cik + Ckj) < Cij → Dij = Dkj y Cij = Cik + Ckj
En caso contrario, dejamos las matrices como están. 
  • Si k ≤ n, aumentamos k en una unidad y repetimos el paso anterior, en caso contrario paramos las iteraciones.
  • La matriz final C contiene los costes óptimos para ir de un vértice a otro, mientras que la matriz D contiene los penúltimos vértices de los caminos óptimos que unen dos vértices, lo cual permite reconstruir cualquier camino óptimo para ir de un vértice a otro.
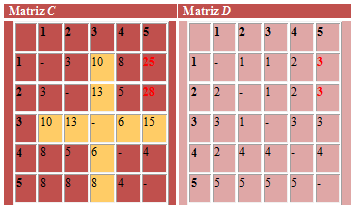
Ejemplo: Aplicar el algoritmo de Floyd sobre el siguiente grafo para obtener las rutas más cortas entre cada dos nodos. El arco (3, 5) es direccional, de manera que no está permitido ningún tráfico del nodo 5 al nodo 3 . Todos los demás arcos permiten el tráfico en ambas direcciones.


Inicializamos las matrices :

Tomamos k=1:

Tomamos i=2 (i ≠k):
  • j=3 (j≠k, j≠i): C[2,1]+C[1,3] = 3+10 = 13 < C[2,3] = ∞, por tanto hacemos:
C[2,3] = 13 y D[2,3] = 1.
  • j=4 (j≠k, j≠i): C[2,1]+C[1,4] = 3+∞ = ∞, no hay que cambiar nada, no podemos llegar de 2 a 4 a través de 1.
  • j=5 (j≠k, j≠i): C[2,1]+C[1,5] = 3+∞ = ∞, no hay que cambiar nada, no podemos llegar de 2 a 5 a través de 1.
  • Tomamos i=3 (i ≠k):
    • j=2 (j≠k, j≠i): C[3,1]+C[1,2] = 10+3 = 13 < C[3,2] = ∞, por tanto hacemos:
C[3,2] = 13 y D[3,2] = 1.
  • j=4 (j≠k, j≠i): C[3,1]+C[1,4] = 10+∞ = ∞, no hay que cambiar nada, no podemos llegar de 3 a 4 a través de 1.
  • j=5 (j≠k, j≠i): C[3,1]+C[1,5] = 10+∞ = ∞, no hay que cambiar nada, no podemos llegar de 3 a 5 a través de 1.
  • Tomamos i=4 (i ≠k):
    • j=2 (j≠k, j≠i): C[4,1]+C[1,2] = ∞+3 = ∞, no hay que cambiar nada, no podemos llegar de 4 a 2 a través de 1.
    • j=3 (j≠k, j≠i): C[4,1]+C[1,3] = ∞+10 = ∞, no hay que cambiar nada, no podemos llegar de 4 a 3 a través de 1.
    • j=5 (j≠k, j≠i): C[4,1]+C[1,5] = ∞+∞ = ∞, no hay que cambiar nada, no podemos llegar de 4 a 5 a través de 1.
Tomamos i=5 (i ≠k), en este caso ocurre como en el paso anterior, como C[5,1]=∞, entonces no habrá ningún cambio, no puede haber ningún camino desde 5 a través de 1.
Tomamos k=2:
Tomamos i=1:
  • j=3: C[1,2]+C[2,3] = 3+13 = 16 > C[1,3] = 10 , por tanto no hay que cambiar nada, el camino es mayor que el existente.
  • j=4: C[1,2]+C[2,4] = 3+5 = 8 < C[1,4] = ∞, por tanto hacemos:
C[1,4] = 8 y D[1,4] = 2 .
  • j=5: C[1,2]+C[2,5] = 3+∞ = ∞, no hay que cambiar nada.
  • Tomamos i=3:
    • j=1: C[3,2]+C[2,1] = 13+3 = 16 > C[3,1] = 10, no hay que cambiar nada.
    • j=4: C[3,2]+C[2,4] = 13+5 = 18 > C[3,4] = 6, no hay que cambiar nada.
    • j=5: C[3,2]+C[2,5] = 13+∞ = ∞, no hay que cambiar nada.
  • Tomamos i=4:
    • j=1: C[4,2]+C[2,1] = 5+3 = 8 < C[4,1] = ∞, por tanto hacemos:
C[4,1] = 8 y D[4,1] = 2.
  • j=3: C[4,2]+C[2,3] = 5+13 = 18 > C[4,3] = 6, no hay que cambiar nada.
  • j=5: C[4,2]+C[2,5] = 5+∞ = ∞, no hay que cambiar nada.
Tomamos i=5, como C[5,2]=∞, entonces no habrá ningún cambio.
Tomamos k=3:

  • Tomamos i=1:
    • j=2: C[1,3]+C[3,2] = 10+13 = 23 > C[1,2] = 3, no hay que cambiar nada.
    • j=4: C[1,3]+C[3,4] = 10+6 = 16 > C[1,4] = 8, no hay que cambiar nada.
    • j=5: C[1,3]+C[3,5] = 10+15 = 25 < C[1,5] = ∞, por tanto hacemos:
C[1,5] = 25 y D[1,5] = 3 .
  • Tomamos i=2:
    • j=1: C[2,3]+C[3,1] = 13+10 = 23 > C[2,1] = 3, no hay que cambiar nada.
    • j=4: C[2,3]+C[3,4] = 13+6 = 19 > C[2,4] = 5, no hay que cambiar nada.
    • j=5: C[2,3]+C[3,5] = 13+15 = 28 < C[2,5] = ∞, por tanto hacemos:
C[2,5] = 28 y D[2,5] = 3.
  • Tomamos i=4:
    • j=1: C[4,3]+C[3,1] = 6+10 = 16 > C[4,1] = 8, no hay que cambiar nada.
    • j=2: C[4,3]+C[3,2] = 6+13 = 19 > C[4,2] = 5, no hay que cambiar nada.
    • j=5: C[4,3]+C[3,5] = 6+15 = 21 > C[4,5] = 4, no hay que cambiar nada.
Tomamos i=5, como C[5,3]=∞, entonces no habrá ningún cambio.
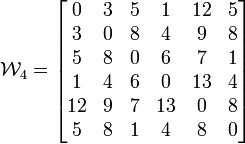
Tomamos k=4:
  • Tomamos i=1:
    • j=2: C[1,4]+C[4,2] = 8+5 = 13 > C[1,2] = 3, no hay que cambiar nada.
    • j=3: C[1,4]+C[4,3] = 8+6 = 14 > C[1,3] = 10, no hay que cambiar nada.
    • j=5: C[1,4]+C[4,5] = 8+4 = 12 < C[1,5] = 25, por tanto hacemos:
C[1,5] = 12 y D[1,5] = 4.
  • Tomamos i=2:
    • j=1: C[2,4]+C[4,1] = 5+8 = 13 > C[2,1] = 3, no hay que cambiar nada.
    • j=3: C[2,4]+C[4,3] = 5+6 = 11 < C[2,3] = 13, por tanto hacemos:
C[2,3] = 11 y D[2,3] = 4.
  • j=5: C[2,4]+C[4,5] = 5+4 = 9 < C[2,5] = 28, por tanto hacemos:
C[2,5] = 9 y D[2,5] = 4.
  • Tomamos i=3:
    • j=1: C[3,4]+C[4,1] = 6+8 = 14 > C[3,1] = 10, no hay que cambiar nada.
    • j=2: C[3,4]+C[4,2] = 6+5 = 11 < C[3,2] = 13, por tanto hacemos:
C[3,2] = 11 y D[3,2] = 4.
  • j=5: C[3,4]+C[4,5] = 6+4 = 10 < C[3,5] = 15, por tanto hacemos:
C[3,5] = 10 y D[3,5] = 4.
  • Tomamos i=5:
    • j=1: C[5,4]+C[4,1] = 4+8 = 12 < C[5,1] = ∞, por tanto hacemos:
C[5,1] = 12 y D[5,1] = 2 .
  • j=2: C[5,4]+C[4,2] = 4+5 = 9 < C[5,2] = ∞, por tanto hacemos:
C[5,2] = 9 y D[5,2] = 4.
  • j=3: C[5,4]+C[4,3] = 4+6 = 10 < C[5,3] = ∞, por tanto hacemos:
C[5,3] = 10 y D[5,3] = 4.
Tomamos k=5:

  • Tomamos i=1:
    • j=2: C[1,5]+C[5,2] = 12+9 = 21 > C[1,2] = 3, no hay que cambiar nada.
    • j=3: C[1,5]+C[5,3] = 12+10 = 22 > C[1,3] = 10, no hay que cambiar nada.
    • j=4: C[1,5]+C[5,4] = 12+4 = 16 > C[1,4] = 8, no hay que cambiar nada.
  • Tomamos i=2:
    • j=1: C[2,5]+C[5,1] = 9+12 = 21 > C[2,1] = 3, no hay que cambiar nada.
    • j=3: C[2,5]+C[5,3] = 9+10 = 19 > C[2,3] = 11, no hay que cambiar nada.
    • j=4: C[2,5]+C[5,4] = 9+4 = 13 > C[2,4] = 5, no hay que cambiar nada.
  • Tomamos i=3:
    • j=1: C[3,5]+C[5,1] = 10+12 = 22 > C[3,1] = 10, no hay que cambiar nada.
    • j=2: C[3,5]+C[5,2] = 10+9 = 19 > C[3,2] = 11, no hay que cambiar nada.
    • j=4: C[3,5]+C[5,4] = 10+4 = 14 > C[3,4] = 6, no hay que cambiar nada.
  • Tomamos i=4:
    • j=1: C[4,5]+C[5,1] = 4+12 = 16 > C[4,1] = 8 , no hay que cambiar nada.
    • j=2: C[4,5]+C[5,2] = 4+9 = 13 > C[4,2] = 5 , no hay que cambiar nada.
    • j=3: C[4,5]+C[5,3] = 4+10 = 14 > C[4,3] = 6, no hay que cambiar nada.
FIN del proceso, las matrices quedan como sigue:
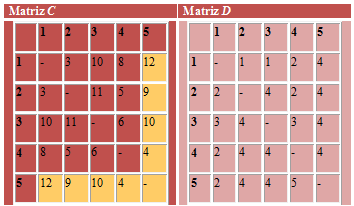
  • Las matrices finales C y D contienen toda la información necesaria para determinar la ruta más corta entre dos nodos cualquiera de la red. Por ejemplo, la distancia más corta del nodo 1 al nodo 5 es C[1,5] = 12.
  • Para determinar la ruta asociada del camino mínimo entre el nodo 1 y el nodo 5 haremos lo siguiente:
    • Consultamos D[1,5]=4, por tanto el nodo predecesor al 5 es el 4, es decir, 4 → 5.
    • Consultamos D[1,4]=2, por tanto el nodo predecesor al 4 es el 2, es decir, 2 → 4 → 5.
Consultamos D[1,2]=1, por tanto el nodo predecesor al 2 es el 1, es decir, 1 → 2 → 4 → 5, y así ya tenemos la ruta completa.
Publicado por en 1 comentario:

Bases Teoricas

Algoritmo de Floyd:


En informática, el algoritmo de Floyd-Warshall, descrito en 1959 por Bernard Roy, es un algoritmo de análisis sobre grafos para encontrar el camino mínimo en grafos dirigidos ponderados. El algoritmo encuentra el camino entre todos los pares de vértices en una única ejecución. El algoritmo de Floyd-Warshall es un ejemplo de programación dinámica.

Aplicaciones:

El algoritmo de Floyd-Warshall puede ser utilizado para resolver los siguientes problemas, entre otros:
  • Camino mínimo en grafos dirigidos (algoritmo de Floyd).
  • Cierre transitivo en grafos dirigidos (algoritmo de Warshall). Es la formulación original del algoritmo de Warshall. El grafo es un grafo no ponderado y representado por una matriz booleana de adyacencia. Entonces la operación de adición es reemplazada por la conjunción lógica(AND) y la operación menor por la disyunción lógica (OR).
  • Encontrar una expresión regular dada por un lenguaje regular aceptado por un autómata finito (algoritmo de Kleene).
  • Inversión de matrices de números reales (algoritmo de Gauss-Jordan).
  • Ruta optima. En esta aplicación es interesante encontrar el camino del flujo máximo entre 2 vértices. Esto significa que en lugar de tomar los mínimos con el pseudocodigo anterior, se coge el máximo. Los pesos de las aristas representan las limitaciones del flujo. Los pesos de los caminos representan cuellos de botella; por ello, la operación de adición anterior es reemplazada por la operación mínimo.
  • Comprobar si un grafo no dirigido es bipartito.

Ejemplo:

Hallar el camino mínimo desde el vértice 3 hasta 4 en el grafo con la siguiente matriz de distancias:
D = \begin{bmatrix} 0 & 3 & 5 & 1 & \infty & \infty\\ 3 & 0 & \infty & \infty & 9 & \infty\\ 5 & \infty & 0 & 7 & 7 & 1\\ 1 & \infty & 7 & 0 & \infty & 4\\ \infty & 9 & 7 & \infty & 0 & \infty\\ \infty & \infty & 1 & 4 & \infty & 0\end{bmatrix}

Aplicamos el algoritmo de Floyd-Warshall, y para ello en cada iteración fijamos un vértice intermedio.

1ª Iteración: nodo intermedio = 1
La matriz es simétrica, por lo que solamente hará falta calcular el triángulo superior de las distancias.
d23 = min(d23, d21 + d13) = 8
d24 = min(d24, d21 + d14) = 4
d25 = min(d25, d21 + d15) = 9
d26 = min(d26, d21 + d16) = \infty
d32 = min(d32, d31 + d12) = 8
d34 = min(d34, d31 + d14) = 6
d35 = min(d35, d31 + d15) = 7
d36 = min(d36, d31 + d16) = 1
d45 = min(d45, d41 + d15) = \infty
d46 = min(d46, d41 + d16) = 4
d56 = min(d56, d51 + d16) = \infty
La matriz de distancia después de esta iteración es:
\mathcal{W}_1 = \begin{bmatrix} 0 & 3 & 5 & 1 & \infty & \infty\\ 3 & 0 & 8 & 4 & 9 & \infty\\ 5 & 8 & 0 & 6 & 7 & 1\\ 1 & 4 & 6 & 0 & \infty & 4\\ \infty & 9 & 7 & \infty & 0 & \infty\\ \infty & \infty & 1 & 4 & \infty & 0\end{bmatrix}
2ª Iteración: nodo intermedio = 2
d13 = min(d13, d12 + d23) = 5
d14 = min(d14, d12 + d24) = 1
d15 = min(d15, d12 + d25) = 12
d16 = min(d16, d12 + d26) = \infty
d34 = min(d34, d32 + d24) = 6
d35 = min(d35, d32 + d25) = 7
d36 = min(d36, d32 + d26) = 1
d45 = min(d45, d42 + d25) = 13
d46 = min(d46, d42 + d26) = 4
d56 = min(d56, d52 + d26) = \infty
La matriz de distancia después de esta iteración es:
\mathcal{W}_2 = \begin{bmatrix} 0 & 3 & 5 & 1 & 12 & \infty\\ 3 & 0 & 8 & 4 & 9 & \infty\\ 5 & 8 & 0 & 6 & 7 & 1\\ 1 & 4 & 6 & 0 & 13 & 4\\ 12 & 9 & 7 & 13 & 0 & \infty\\ \infty & \infty & 1 & 4 & \infty & 0\end{bmatrix}
3ª Iteración: nodo intermedio = 3
d12 = min(d12, d13 + d32) = 3
d14 = min(d14, d13 + d34) = 1
d15 = min(d15, d13 + d35) = 12
d16 = min(d16, d13 + d36) = 6
d24 = min(d24, d23 + d34) = 4
d25 = min(d25, d23 + d35) = 9
d26 = min(d26, d23 + d36) = 9
d45 = min(d45, d43 + d35) = 13
d46 = min(d46, d43 + d36) = 4
d56 = min(d56, d53 + d36) = 8
La matriz de distancia después de esta iteración es:
\mathcal{W}_3 = \begin{bmatrix} 0 & 3 & 5 & 1 & 12 & 6\\ 3 & 0 & 8 & 4 & 9 & 9\\ 5 & 8 & 0 & 6 & 7 & 1\\ 1 & 4 & 6 & 0 & 13 & 4\\ 12 & 9 & 7 & 13 & 0 & 8\\ 6 & 9 & 1 & 4 & 8 & 0\end{bmatrix}
4ª Iteración: nodo intermedio = 4
d12 = min(d12, d14 + d42) = 3
d13 = min(d13, d14 + d43) = 5
d15 = min(d15, d14 + d45) = 12
d16 = min(d16, d14 + d46) = 5
d23 = min(d23, d24 + d43) = 8
d25 = min(d25, d24 + d45) = 9
d26 = min(d26, d24 + d46) = 8
d35 = min(d35, d34 + d45) = 7
d36 = min(d36, d34 + d46) = 1
d56 = min(d56, d54 + d46) = 8
La matriz de distancia después de esta iteración es:
\mathcal{W}_4 = \begin{bmatrix} 0 & 3 & 5 & 1 & 12 & 5\\ 3 & 0 & 8 & 4 & 9 & 8\\ 5 & 8 & 0 & 6 & 7 & 1\\ 1 & 4 & 6 & 0 & 13 & 4\\ 12 & 9 & 7 & 13 & 0 & 8\\ 5 & 8 & 1 & 4 & 8 & 0\end{bmatrix}
5ª Iteración: nodo intermedio = 5
d12 = min(d12, d15 + d52) = 3
d13 = min(d13, d15 + d53) = 5
d14 = min(d14, d15 + d54) = 1
d16 = min(d16, d15 + d56) = 5
d23 = min(d23, d25 + d53) = 8
d24 = min(d24, d25 + d54) = 4
d26 = min(d26, d25 + d56) = 8
d34 = min(d34, d35 + d54) = 6
d36 = min(d36, d35 + d56) = 1
d46 = min(d46, d45 + d56) = 4
La matriz de distancia después de esta iteración es:
\mathcal{W}_5 = \mathcal{W}_4 = \begin{bmatrix} 0 & 3 & 5 & 1 & 12 & 5\\ 3 & 0 & 8 & 4 & 9 & 8\\ 5 & 8 & 0 & 6 & 7 & 1\\ 1 & 4 & 6 & 0 & 13 & 4\\ 12 & 9 & 7 & 13 & 0 & 8\\ 5 & 8 & 1 & 4 & 8 & 0\end{bmatrix}
6ª Iteración: nodo intermedio = 6
d12 = min(d12, d16 + d62) = 3
d13 = min(d13, d16 + d63) = 5
d14 = min(d14, d16 + d64) = 1
d15 = min(d15, d16 + d65) = 12
d23 = min(d23, d26 + d63) = 8
d24 = min(d24, d26 + d64) = 4
d25 = min(d25, d26 + d65) = 9
d34 = min(d34, d36 + d64) = 5
d35 = min(d35, d36 + d65) = 7
d45 = min(d45, d46 + d65) = 12
La matriz de distancia después de esta iteración es:
\mathcal{W}_6 = \begin{bmatrix} 0 & 3 & 5 & 1 & 12 & 5\\ 3 & 0 & 8 & 4 & 9 & 8\\ 5 & 8 & 0 & 5 & 7 & 1\\ 1 & 4 & 5 & 0 & 12 & 4\\ 12 & 9 & 7 & 12 & 0 & 8\\ 5 & 8 & 1 & 4 & 8 & 0\end{bmatrix}
Ya se han hecho todas las iteraciones posibles. Por tanto, el camino mínimo entre 2 vértices cualesquiera del grafo será el obtenido en la matriz final. En este caso, el camino mínimo entre 3 y 4 vale 5.


Publicado por en 2 comentarios:

miércoles, 13 de febrero de 2013

Video Tutorial

http://www.youtube.com/watch?v=rEp50y6Ul44


Publicado por en No hay comentarios:
Suscribirse a: Entradas (Atom)